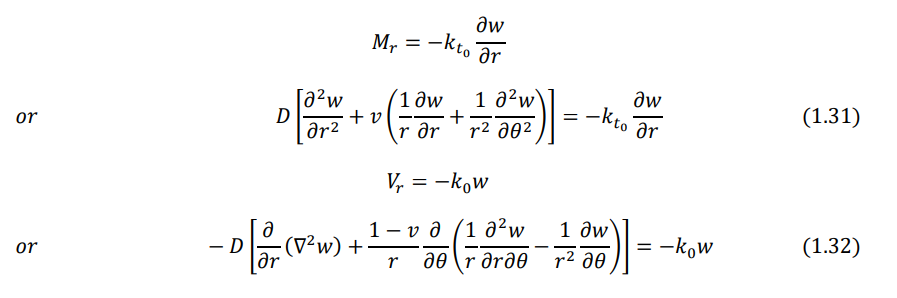EXPERIMENTAL METHODOLOGY

EQUATION OF MOTION: CLASSICAL PLATE THEORY

1.1 Equation of Motion

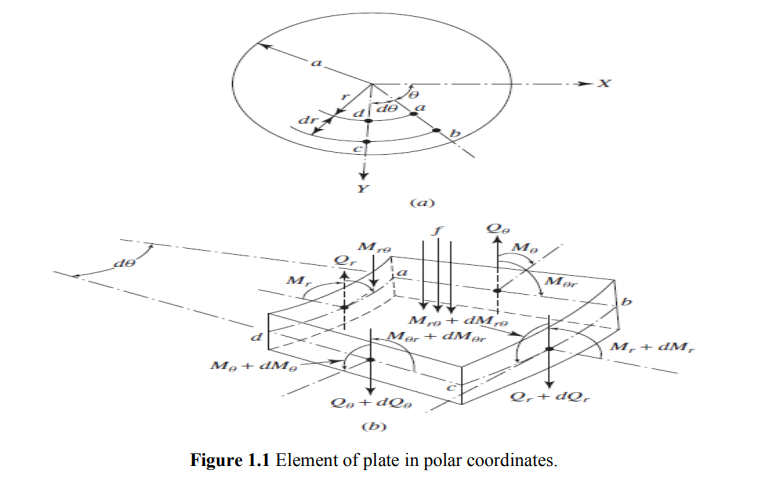
Consider an infinitesimal element of the plate in polar coordinates as shown in Fig. 1.1. In this figure the radial moment M_r, tangential moment M_θ, twisting moments M_rθ and M_θr, and the transverse shear forces Q_r and Q_θ, are shown on the positive and negative edges of the element. The equations of motion of the plate can be derived in polar coordinates by considering the dynamic equilibrium of the element shown in Fig. 1.1 as follows: Moment equilibrium about the tangential (θ) direction:

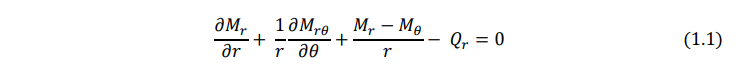
Moment equilibrium about the radial (R) direction:

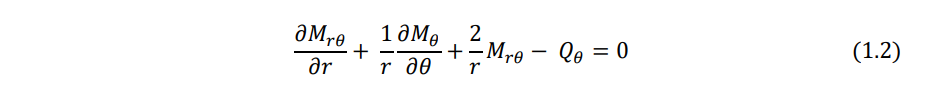
Force equilibrium in the z direction:

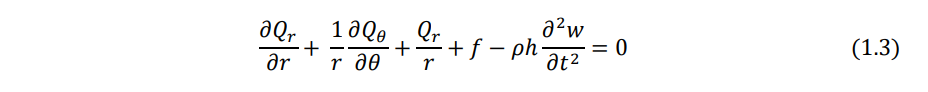
Equations (1.1)-(1.3) can be combined to derive a single equation of motion in terms of the moment resultants M_r, M_θ, and M_rθ, By substituting the moment resultants in terms of the transverse displacement w, the final equation of motion, shown in Eq. (1.16), can be obtained.

The coordinate transformation technique can also be used to derive the equation of motion in polar coordinates from the corresponding equation in Cartesian coordinates, as indicated below.

1.2 Transformation of Relations

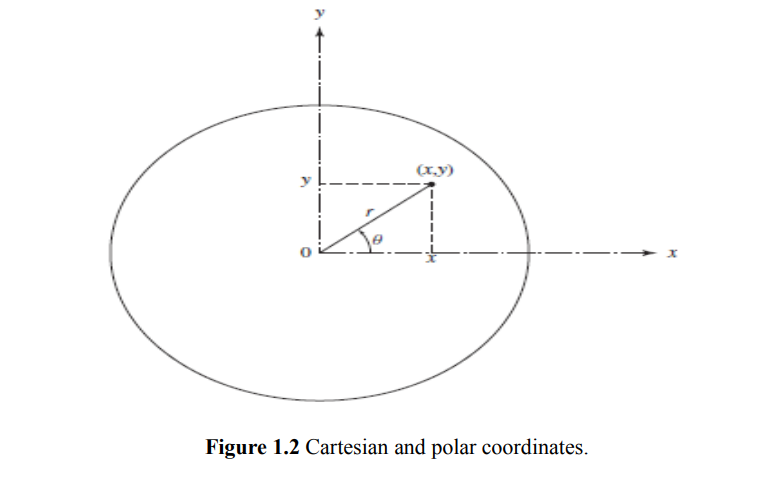
The Cartesian and polar coordinates of a point P are related as (Fig. 1.2)

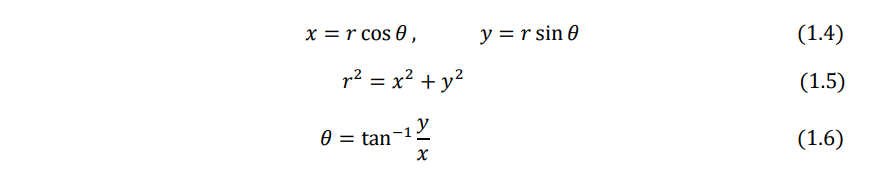
From Eqs. (1.5) and (1.6), we obtain

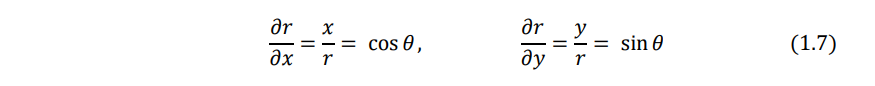
Similarly, Eqs. (1.6) and (1.4) give

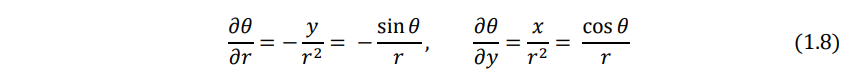
Since the deflection of the plate w is a function of r and θ, the chain rule of differentiation yields

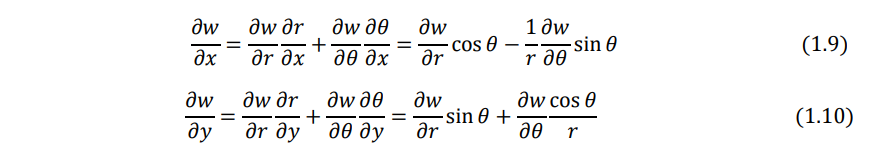
For the expressions ∂²w ∕ ∂x², ∂² w ∕ ∂x∂y , and ∂ ²w ∕ ∂y², the operations ∂/∂x and ∂/∂y of Eqs. (1.9) and (1.10) are repeated to obtain

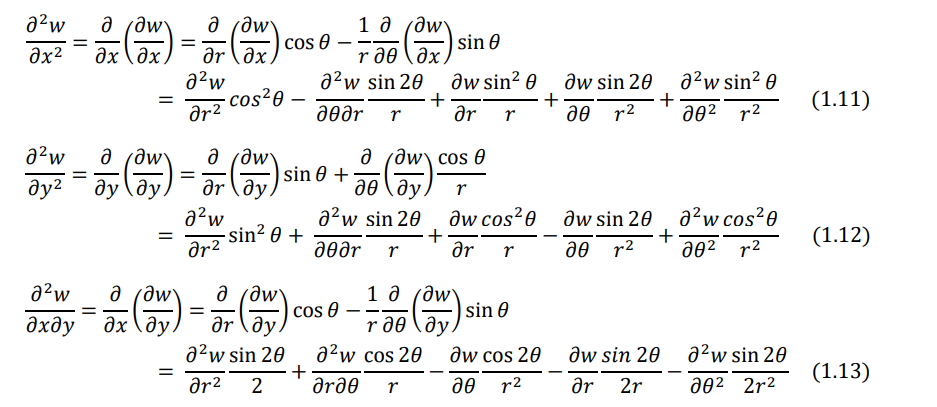
By adding Eqs. (1.11) and (1.12), we obtain

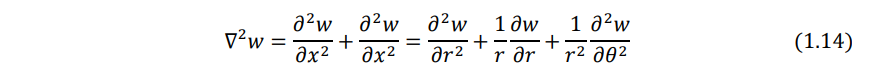
By repeating the operation ∇² twice, we can express

Using Eqs. (1.9), (1.10), and (1.11) in the equation of motion for the forced transverse vibration of a circular plate can be expressed as

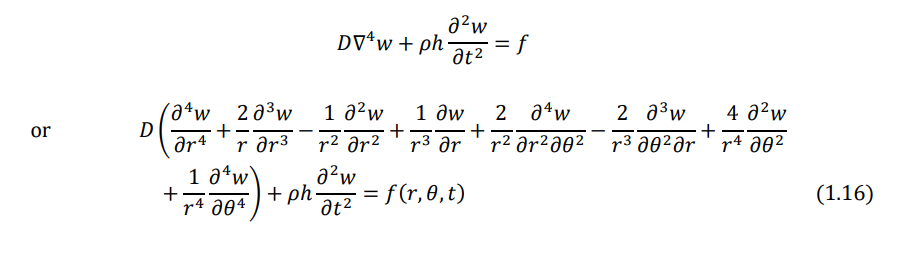
1.3 Moment and Force Resultants

Using the transformation procedure, the moment resultant - transverse displacement relations can be obtained as:

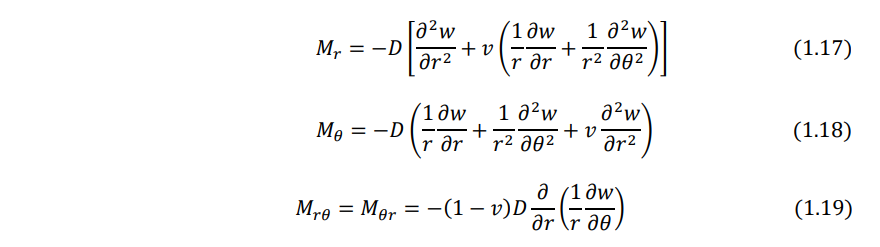
Similarly, the shear force resultants can be expressed as

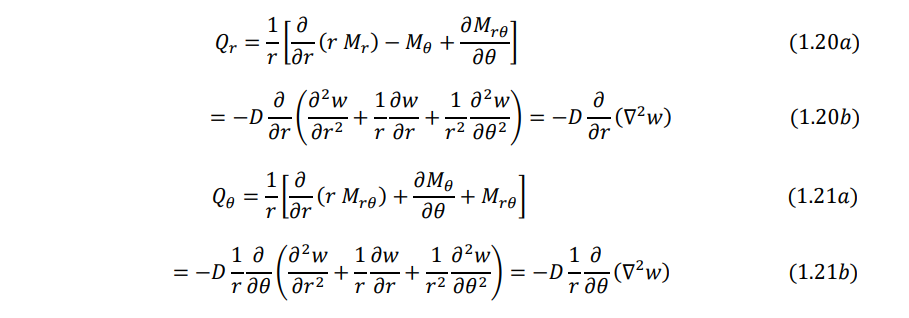
The effective transverse shear forces can be written as

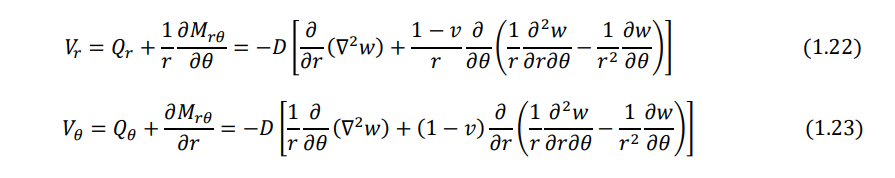
Note that the Laplacian operator appearing in Eqs. (1.20) - (1.23) is given in polar coordinates by Eq. (1.14).

1.4 Boundary Conditions

1. Clamped, fixed, or built-in edge. The deflection and slope (normal to the boundary) must be zero:

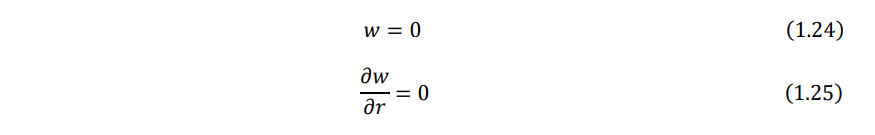
where r denotes the radial (normal) direction to the boundary.

2. Simply supported edge. The deflection and bending moment resultant must be zero:

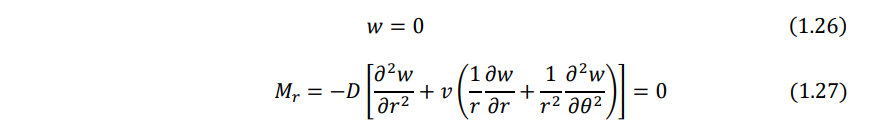
3. Free edge. The bending moment resultant and the effective shear force resultant on the edge must be zero:

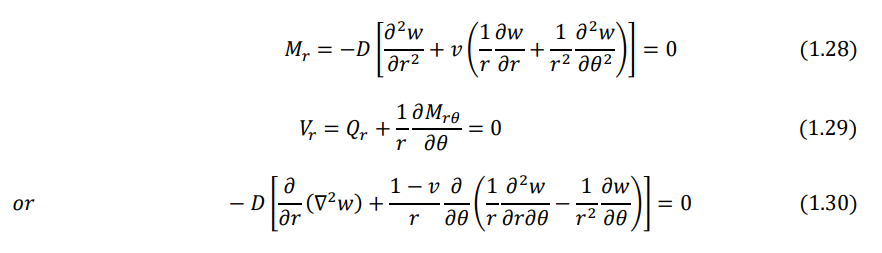
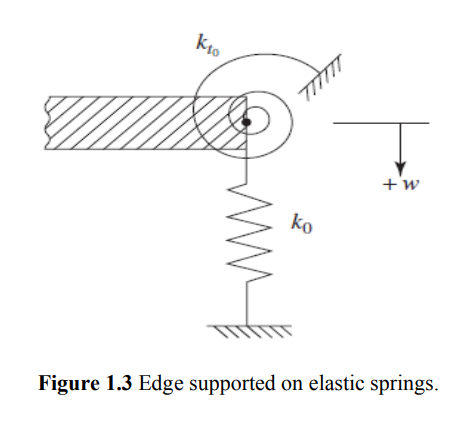
4. Edge supported on elastic springs. If the edge is supported on linear and torsional springs all around as shown in Fig. 1.3, the boundary conditions can be stated as follows: